Our Research
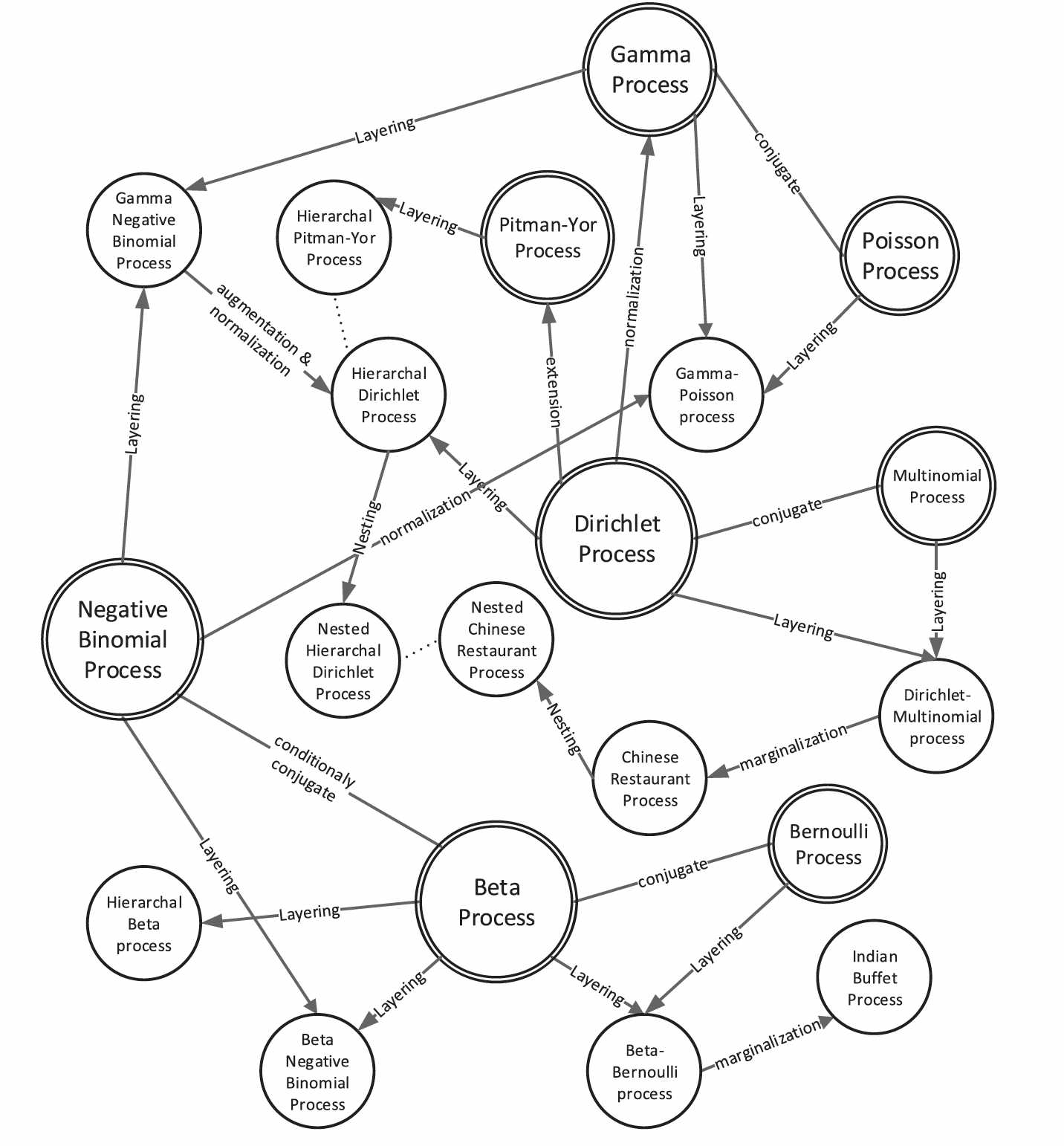
Bayesian Nonparametric Learning
The core of Bayesian nonparametric learning lies in the operations of stochastic processes. We have proposed several innovative ideas in this aspect, such as dependent Indian buffet processes, network correlated thinned gamma processes, and cooperation between Dirichlet processes or gamma processes. These works have enhanced the ability to model more complex data and tasks, including concept drift, causal inference, and negative sampling.

Bayesian Deep Learning
We recently introduced stochastic processes (e.g., Gaussian processes) as functional prior for Bayesian neural networks and achieved function-space posterior inference under Wasserstein distance. This approach proved effective in resolving the pathologies of weight-space inference and providing stronger uncertainty modelling.
Diffusion Bridge and Flow Matching
We are investigating the application of diffusion bridges and flow matching within function space, aiming to develop efficient sampling strategies that enhance both theoretical understanding and practical performance. This research explores how these probabilistic tools can be leveraged to model complex functional distributions and improve inference in infinite-dimensional settings. By focusing on function space representations, we seek to uncover novel insights into the dynamics of sampling processes and contribute to the broader field of probabilistic machine learning.
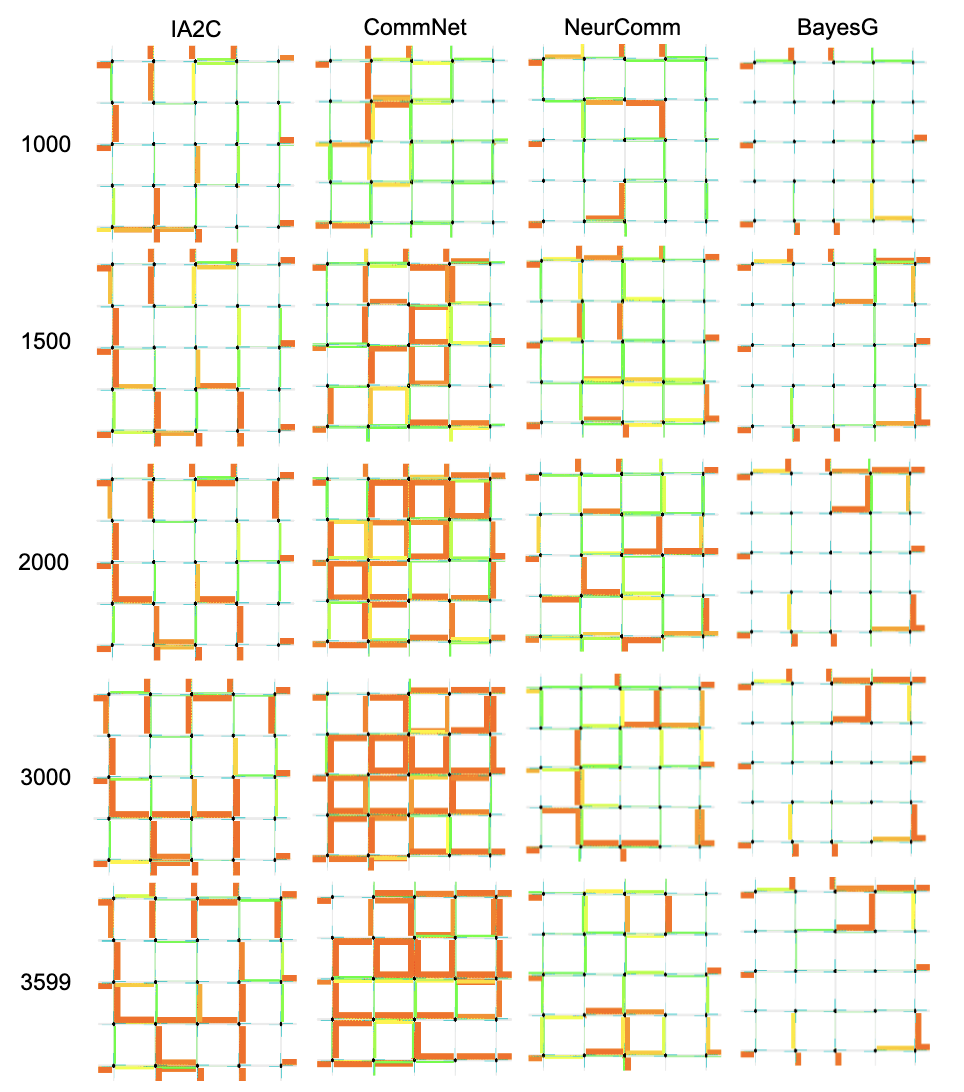
Deep Reinforcement Learning
We proposed a series of uncertainty-oriented ideas to enable the deep reinforcement learning to work in complex but practical scenarios, such as Bayesian agent graph inference for the environments with constrained observability and communication, and automatically adapting to the non-stationary environments without any boundary information.
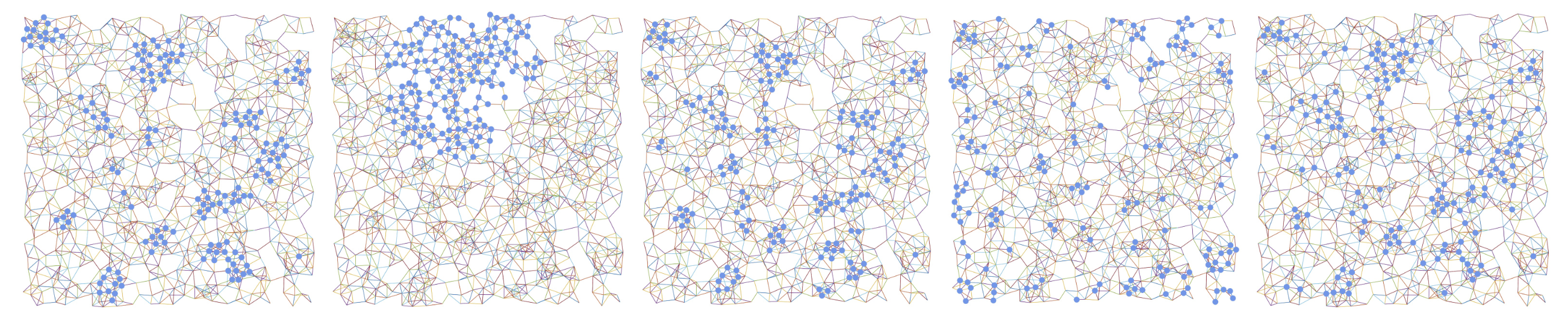
Graph Neural Networks
We proposed a new quantum physics-inspired graph neural network, where the position/momentum uncertainty of nodes modelled using the path integral formulation for novel graph convolution and pooling. We also initiated a novel graph convolution with negative samples via determinant point processes which proved effective in reducing the risk of over-smoothing and over-squashing.

Web and Text Mining
We have proposed innovative ways to represent news events and documents by networks/graphs and analyzed the properties of news events and documents by examining their corresponding networks/graphs, e.g., degree distribution, max spanning tree and small-world properties. In all works in this area, uncertainty has been the breakthrough point with high priority, such as studying information network uncertainty which was theoretically linked to the power-law property of the network for the evolution estimation of news events on the web.